Introduction to Theory of Computation 2장_1,2,3 용어/개념정리
Chapter 2. Finite Automata and Regular Languages
p.30 자판기 오토마타 설명

p.31
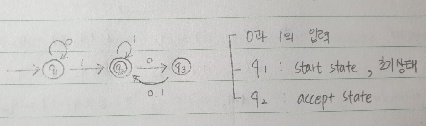
q₁ : start state
q₂ : accept state
(ex) 1101은 accept 된다. / 000110은 reject 된다.
>> w : 1로 끝나는 스트링은 accept 된다. / 0이 짝수개가 나오는 스트링은 accept 된다.
< DFA >
: Deterministic Finite Automata
(정의) A dif is a 5-tuple M = (Q, ∑, δ, q, F)
//원소가 5개인 순서쌍
- Q : set of states / 유한 상태의 집합
- ∑ : alphabet, set of symbols / 문자들의 유한집합, 입력 알파벳
- δ : transition function / 전체 함수, 전이 함수
( δ = Q x ∑ → Q )
- q : q ∈ Q, start state /초기 상태
- F : F ⊆ Q, set of accept states /종료 상태들의 집합
(예제) M = (Q, ∑, ∂, q, F)에서 Q = {q₁, q₂, q₃}, ∑ = {0 ,1}, δ = δ₁, F = {g₂} 일 때, 순서쌍과 테이블로 표현하라.
δ₁( q₁, 0 ) = q₁ δ₁( q₁, 1 ) = q₂
δ₁( q₂, 0 ) = q₃ δ₁( q₂, 1 ) = q₂
δ₁( q₃, 0 ) = q₂ δ₁( q₃, 1 ) = q₂
| 0 | 1 | |
| q₁ | q₁ | q₂ |
| q₂ | q₃ | q₂ |
| q₃ | q₂ | q₂ |
< L(M) >
: L(M) is the set of all strings accepted by M.
L(M) = { f= w | w is a string over ∑ and Μ accepted w. }
< Regular Language >
: A language is called regular.
if there exists a DFA M such that A=L(M).
DFA를 통해 결과(accept, reject)를 얻을 수 있는데, 이것을 "언어"라고 하자.
정규 언어란?
유한 상태 기계로 인식 가능한 언어가 Regular Language(정규 언어)이며,
DFA(Deterministic Finite Automata)/NFA(Nondeterministic Finite Automata)가 유한 상태 기계에 속하는 오토마톤이다.
(예제 1) A = { w : w는 홀수 1을 포함한 이진 string이다. }
A = { w∈{1,2} | w contains odd 1's. }
A는 "정규언어"이다.
(※ A=L(M)를 만족하므로 A가 L(M)에 속하는지 증명)
M = (Q, ∑, ∂, q, F)에서 Q = {q₁,q₂}이며, q₁는 홀수, q₂는 짝수를 읽는다. 또한 ∑={0,1}, F={q₂}이다.

//1의 개수, 1의 개수를 세고 있는 것이 아닌 "상태(state)"를 통해 accept, reject를 확인한다.
위의 테이블과 DFA를 통해 language A를 통해 accept되는 Finite Automaton임을 알 수 있다.
∴ 따라서 A는 정규언어이다.
(예제 2)
A = { w : w는 substring 101이 포함된 이진 string이다. }
=> A = { w∈{0,1}* | w contains 101 as a substring. }
A는 "정규언어"이다.
(※ A=L(M)를 만족하므로 A가 L(M)에 속하는지 증명)

위의 테이블과 DFA를 통해 language A를 통해 accept되는 Finite Automaton임을 알 수 있다.
∴ 따라서 A는 정규언어이다.
< Regular Operation >
Let A and B be language over same ∑.
두개의 language의 연산을 통해서 새로운 언어를 만들 수 있다.
AB = {ww′: w ∈ A and w′ ∈ B}.
A∗ = {u1 u2... uk : k ≥ 0 and ui ∈ A for all i = 1, 2,... , k}. //추가적으로 λ(empty string) ∈ A∗
(ex) A = {10, 01}, B = {λ, 0, 1}
AB = {10, 100, 101, 01, 010, 011}
AA = A², A²A = A³
//합집합과 교집합 역시 집합의 연산이기 때문에 Regular Operation에 속한다.
<Union Operation>

Theorem 2.3.1. The set of regular languages is closed under the union operation, i.e., if A and B are regular languages over the same alphabet ∑ , then A∪B is also a regular language.
// Regular Language는 Union Operation에 의해 닫혀져 있다.
// 같은 알파벳 ∑에 있는 A, B가 정규 언어라면 A∪B 또한 정규 언어이다.
----------------------------------------------------------------------------------------------------------------------------------------------------
**복습**
< DFA란 >
A DFA is a 5-tuple. M = (Q, ∑, δ, q, F)
- Q : a set of states.
- ∑ : a set of symbols.
- δ : transition function. // δ : Q x (∑ ∪ {ε}) -> δ(Q)
// 현재 상태에서 λ(empty string)을 포함한 모든 symbol을 따르는 과정
- q ∈ Q : start state.
- F ⊆ Q : a set of accept state.
(예제) M = (Q, ∑, δ, q, F)일 때, M = ({1,2,3,4}, {0,1}, δ, {1}, {4}}이다. Diagram을 그리고, w를 구하라.

L(M) = { w ∈ {0,1}*, w contains 11 or 101. }
< DFA 성질 >
: 하나의 정의역에 대해 오직 한 쌍의 공역이 존재한다.
(= 가야할 곳이 유일함, deterministic 하다.)
(예제)
M = (Q, ∑, δ, q, F) 에서, {w ∈ {0,1}* | w has a 1 in the 3rd position from the right}이다.
// 뒤(오른쪽)에서 세번째 글자가 1인 string.

마지막 세 글자를 기억하는 경우의 수 = 8가지. 예시로, 000인 상태에서 0을 읽으면 000. 1을 읽으면 001이다.
(※start state가 00, 01, 10, 11이기 때문에 어떠한 상태를 시작 state로 잡아도 상관이 없음.)
'학교 공부 > 계산이론' 카테고리의 다른 글
| Introduction to Theory of Computation 2장_7,8 정리/설명 (0) | 2019.10.10 |
|---|---|
| Introduction to Theory of Computation 2장_6 정리/설명 (2) | 2019.10.10 |
| Introduction to Theory of Computation 2장_4,5 용어/개념정리 (0) | 2019.09.29 |
| Introduction to Theory of Computation 1장_2 문제풀이 (0) | 2019.09.14 |
| Introduction to Theory of Computation 1장_2 용어,개념정리 (1) | 2019.09.13 |


댓글