<< 이산수학 10주차 >>
언어, 문법, 오토마타의 관계를 이해해야 한다.
언어는 문자열들을 정의 -> 문법은 언어에 속한 문자열들을 생성 -> 오토마타는 문자열들을 승인
자연어? 정형언어?
우리는 c, java와 같이 기계 처리를 할 수 있는 정형 언어를 배울 것이다.
언어란?
문자열들의 집합이다. ∑를 기호들의 집합이라고 한다. ∑*는 그럼 모든 문자열의 집합이다. 언어 L∈∑*이다.
(*는 공집합까지 포함하므로 λ∈∑*로 표현할 수 있다.)
정규문자의 존재?
∑ = {a,b}
L1 = {(ab)ⁿ | n≥0}= (ab)*
L2 = {aⁿ | n≥0} = a*
L3 = {aⁿbⁿ | n≥0} ≠ (a*b*)이기 때문 // 정규 표현 부재
언어의 결합
두 언어 L1과 L2의 결합 L1L2는 {uv | u∈L1, v∈L2}
Q. ∑ = {a,b,c} 언어X={aa,ab} Y={a,ca,λ}의 결합 XY를 구하시오.
XY = {aaa, aaca, aa, aba, caab, ab}
언어의 곱
언어 L의 n번 곱을 Lⁿ으로 표기한다.
Q. L={a, ca, λ}
L^0 = {λ}
L^2 = {aa, aca, a, caa, caca, ca, λ}
L^3 = {aaa, acaa, ... }
클린 스타 클로우져
: L*를 L의 클리네 스타 클로우져라고 부른다. 언어 공간을 정의한다.
람다(λ)도 포함한다. 하지만 클리네 플러스 클로우져 L+는 λ를 제외시킨다. 예로 id, pwd가 있다.
★문법★
: 언어에 속하는 문자열을 생성하는 규칙이다.
| 문법 G = (N, T, S, P) N : 비단말(non-terminal)기호, 반드시 다른 것으로 치환되어야한다. T : 단말(Terminal)기호, 더 이상 다른 것으로 치환될 수 없음. S : 시작을 나타내는 비단말 기호 P : 생성 규칙이다. |
- 모든 기호 V = N∪T이다.
- 비 단말 기호와 단말기호는 겹치지 않는다. N∩T = 공집합
- 시작 기호는 비단말 기호 중에 하나이다. S∈N
-★ 생성되는 문자열을 단말 기호들로만 구성한다. w∈T* ★
문자열 생성
: 한 번에 하나씩 생성 규칙을 적용한다.
- S =>* w
- S는 시작 기호이다.
- w∈T*
즉, 시작 기호에서 출발해서 문자열 w를 생성한다.
(예제)
S -> ABa
A -> BB
B -> ab
AB -> b
S=> ABa=> ba 따라서 S=>*ba이다.
S=> ABa=> BBBa=> abBBa=> ababBa=> abababa 따라서 S=>* abababa이다.
문법에 의해 생성된 언어
: 문법 G = (N, T, S, P)에 의하여 생성되는 모든 문자열 모임
L(G) = { w∈T* | S =>* w }
(예제)
G = (N, T, S, P)
N = {S, A}
T = {a, b}
P = {S->aA, S->b, A->aa}
L(G) = {b, aaa}
(예제)
G = (N, T, S, P)
N = {S}
T = {0, 1}
P = {S-> 11S, S->0}
L(G) = {0, 110, 11110, ... } = {(11)ⁿ0 | n≥0} = (11)*0
위의 예제들과 반대로
L = {aⁿbⁿ | n≥0}을 생성하는 문법은?
P = {S->aSb, S->λ}
L = {(a^m)(b^n) | m, n ≥0}을 생성하는 문법은?
P = {S->0S, S->S1, S->λ}
언어와 문법의 분류
노암 촘스키의 분류 체계
type 0 무제약 언어 // 문법의 생성 규칙이 존재 X
type 1 문맥 민감 언어
type 2 문맥 자유 언어
type 3 정규 언어
>> 컴퓨터 처리가 가능한 경계선은 type 2이다. 문맥 자유 언어와 정규 언어에서는 잘 다뤄짐.
★문법 분류★
생성 규칙에 따라서 분류한다.
w1은 왼쪽을 의미한다.
① |w1|≥2 인 경우
type 0일 경우, 왼쪽, 오른쪽 아무런 제약이 없다.
type 1일 경우, xw1y -> xw2y 형식이다. //좌우에 x, y가 있을 때 치환된다.
x, y가 공백 문자열일 수도 있다.
② |w1|=1 인 경우
type 2일 경우, 아무런 제약이 없다.
type 3일 경우, 오른쪽에 제약이 존재한다. // 비 단말 기호가 나온다면 오른쪽 끝이나 왼쪽 끝에
(예제)
L = {(a^m)(b^n) | m, n≥0}을 생성하는 문법은?
N = {S}
T = {a, b}
S
P = {S->aS, S->Sb, S->λ}
>> type 3에 해당하는 정규 문법이다.
(예제)
L = {(a^n)(b^n) | n≥0}을 생성하는 문법은?
N = {S}
G = {a, b}
S
P = {S->aSb, S->λ}
>> type 2에 속하는 문맥 자유 문법이다.
(예제)
L = {0ⁿ1ⁿ2ⁿ | n=0,1,2,3,... }
N = {S}
G = {0,1,2}
S
P = {S->0 SAB, S->λ, BA->AB, 0A->01, 1A->11, 1B->12, 2B->22}
>> type 0에 속한다.
정규 언어 vs 문맥 자유 언어
- 정규 언어 : 로그인 혹은 비밀번호에 사용되는 언어
- 문맥 자유 언어 : C, JAVA와 같이 컴파일 시간이 걸리지만, 다양한 제어 구조를 표현한다.
>> 문자열을 생성할 때 문법을 이용해 유도 트리(파스 트리, 구문 트리)를 만들 수 있다.
BNF : type 2(당연히 type 3) 문법을 표현하는 다른 방법
기존 생성 규칙을 BNF로 표현
A->Aa, A->a, A->AB
BNF 표현) <A> := <A>a | a | <A><B>
- 괄호는 비 단말 기호
- 괄호가 없으면 비단말 기호
- := 치환
- | 선택
유한 상태 오토마타(FSA)
: 입력 문자열의 accept 혹은 reject 여부를 판단한다.
이를 위해서 최종 상태가 약속되어 있어야 한다.
- DFA
- NFA
DFA(Deterministic Finite state Automata)
| A = (Q, ∑, δ, q0, F) Q : 상태 ∑ : 입력 δ : 상태 전이 함수, Q x ∑ -> Q 함수의 정의가 결정적이다. 상태 전이 함수는 상태 전이 표와 다이아그램으로도 표현한다. q0 ∈ Q : start state F ∈ Q : accept state |
(예제)
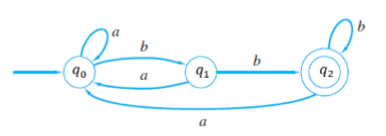
δ(q0, a) = q0
δ(q1, a) = q0
δ(q2, a) = q0
δ(q0, b) = q1
δ(q1, b) = q2
δ(q2, b) = q2
// accept 혹은 reject를 확인할 수 있다.
DFA 설계
- a가 전혀 없는 스트링만을 승인하는 DFA 설계
- a가 홀수개인 스트링만 승인하는 DFA 설계
- a가 짝수개인 스트링만 승인하는 DFA 설계
오토마타 간의 동치
: 똑같은 스트링을 승인하면 동치이다.
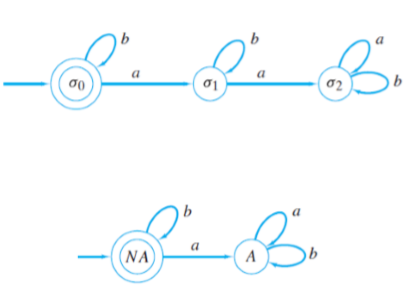
// 알고리즘을 짠다면?
input : 문자열 n
output : accept 혹은 reject
언어 인식
: L(A)는 오토마타 A = (Q, ∑, δ, q0, E)에 의해 승인되는 스트링 집합
L(A) = {w∈∑* | δ*(q0, w) ∈ F}
(예제. 오토마타 -> 문자열)
- L(A)는 0 이후에 바로 1이 나오는 모든 스트링을 승인한다.
- L(A) = { λ, 1, 11, 111, ... } = {(1)ⁿ | n≥0}
- L(A) = {0, 01}
- L(A) = {(0)ⁿ | n≥0 혹은 010}
(예제. 문자열 -> 오토마타)
- 두 개의 0으로 시작하는 비트 문자열 집합
- 두 개의 연속적인 0을 포함하는 비트 문자열 집합
- 두 개의 연속적인 0을 포함하지 않는 비트 문자열 집합
- 홀수 개의 1을 포함하고 최소 두 개의 연속적인 0으로 끝나는 비트 문자열을 인식하는 DFA
(예제. 동치)
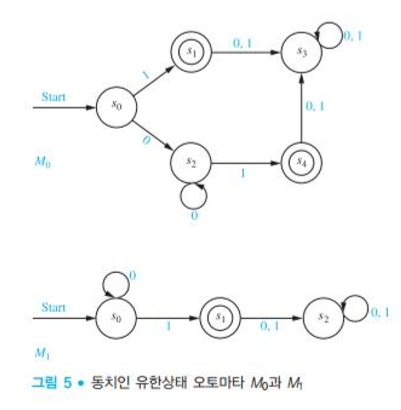
NFA(Nondeterministic Finite state Automata)
| A = (Q, ∑, δ, q0, F) Q : 상태 ∑ : 입력 δ : 상태 전이 함수, Q x ∑ -> 2^Q //멱집합 q0 ∈ Q : start state F ∈ Q : accept state |
(예제)
Q = {q0, C, Z}
∑ = {a, b}
S = q0
F = {Z}
δ(q0, a) = {C}

δ(q0, b) = {q0}
δ(C, a) = 공집합
δ(C, b) = {C, Z} // 다음 상태는 C, Z 둘 중 하나인데 어딘지는 모름.
δ(Z, a) = 공집합
δ(Z, b) = 공집합
(예제)

>> L(A) = { 0*| 0*01 | 1*01 }
언어와 문법, 오토마타
- L은 문자 열의 집합을 정의한 언어이다.
- L(G)는 문법 G=(N,T,S,P)에 의하여 생성되는 모든 문자열 집합이다.
// L(G) = {w∈T* | S=>* w}
- L(A)는 오토마타 A=(Q, ∑, δ, q0, F)로 승인되는 모든 문자열 집합
// L(A) = { w∈∑* | δ*(q0, w)∈F }
'학교 공부 > 이산수학' 카테고리의 다른 글
| [이산수학] 정규언어, 정규표현 (0) | 2020.06.02 |
|---|---|
| [이산수학] 님(nim) 게임 (0) | 2020.05.14 |
| [이산수학] 최소 신장트리와 프림/크루스칼 알고리즘 (0) | 2020.05.06 |
| [이산수학] 방향그래프, 그래프 탐색과 구현 (0) | 2020.05.06 |
| [이산수학] 외판원문제(TSP문제)와 그래프 동형 (0) | 2020.05.06 |




댓글